800 (number)

This article is about the number 800. For the Common Era Year 800, see 800. For other uses, see 800 (disambiguation)

800 (eight hundred) is the natural number following 799 and preceding 801.

List of numbers — Integers ← 0 100 200 300 400 500 600 700 800 900 →
Cardinal	800 eight hundred
Ordinal	800th eight hundredth
Factorization	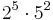$2^5 \cdot 5^2$
Roman numeral	DCCC
Roman numeral (Unicode)	DCCC, dccc
Binary	1100100000
Octal	1440
Duodecimal	568
Hexadecimal	320

It is the sum of four consecutive primes (193 + 197 + 199 + 211). It is a Harshad number.

801 = 3² × 89, Harshad number

802 = 2 × 401, sum of eight consecutive primes (83 + 89 + 97 + 101 + 103 + 107 + 109 + 113), nontotient

803 = 11 × 73, sum of three consecutive primes (263 + 269 + 271), sum of nine consecutive primes (71 + 73 + 79 + 83 + 89 + 97 + 101 + 103 + 107), Harshad number

804 = 2² × 3 × 67, nontotient, Harshad number

805 = 5 × 7 × 23

806 = 2 × 13 × 31, sphenic number, nontotient, totient sum for first 51 integers

807 = 3 × 269

808 = 2³ × 101, strobogrammatic number

809 prime number, Sophie Germain prime, Chen prime, Eisenstein prime with no imaginary part

810 = 2 × 3⁴ × 5, Harshad number

811 prime number, sum of five consecutive primes (151 + 157 + 163 + 167 + 173), Chen prime, Mertens function(811) returns 0

812 = 2² × 7 × 29, pronic number, Mertens function(812) returns 0

813 = 3 × 271

814 = 2 × 11 × 37, sphenic number, Mertens function(814) returns 0, nontotient

815 = 5 × 163

816 = 2⁴ × 3 × 17, tetrahedral number, member of the Padovan sequence, Zuckerman number

817 = 19 × 43, sum of three consecutive primes (269 + 271 + 277), centered hexagonal number

818 = 2 × 409, nontotient

819 = 3² × 7 × 13, square pyramidal number

820 = 2² × 5 × 41, triangular number, Harshad number

821 prime number, twin prime, Eisenstein prime with no imaginary part, prime quadruplet with 823, 827, 829

822 = 2 × 3 × 137, sum of twelve consecutive primes (43 + 47 + 53 + 59 + 61 + 67 + 71 + 73 + 79 + 83 + 89 + 97), sphenic number, member of the Mian–Chowla sequence

823 prime number, twin prime, Mertens function(823) returns 0, prime quadruplet with 821, 827, 829

824 = 2³ × 103, sum of ten consecutive primes (61 + 67 + 71 + 73 + 79 + 83 + 89 + 97 + 101 + 103), Mertens function(824) returns 0, nontotient

825 = 3 × 5² × 11, Smith number, Mertens function(825) returns 0, Harshad number

826 = 2 × 7 × 59, sphenic number

827 prime number, twin prime, part of prime quadruplet with {821, 823, 829}, sum of seven consecutive primes (103 + 107 + 109 + 113 + 127 + 131 + 137), Chen prime, Eisenstein prime with no imaginary part, strictly non-palindromic number

828 = 2² × 3² × 23, Harshad number

829 prime number, twin prime, part of prime quadruplet with {827, 823, 821}, sum of three consecutive primes (271 + 277 + 281), Chen prime

830 = 2 × 5 × 83, sphenic number, sum of four consecutive primes (197 + 199 + 211 + 223), nontotient, totient sum for first 52 integers

831 = 3 × 277

832 = 2⁶ × 13, Harshad number

833 = 7² × 17

834 = 2 × 3 × 139, sphenic number, sum of six consecutive primes (127 + 131 + 137 + 139 + 149 + 151), nontotient

835 = 5 × 167, Motzkin number

836 = 2² × 11 × 19, weird number

837 = 3³ × 31

838 = 2 × 419

839 prime number, safe prime, sum of five consecutive primes (157 + 163 + 167 + 173 + 179), Chen prime, Eisenstein prime with no imaginary part, highly cototient number

840 = 2³ × 3 × 5 × 7, highly composite number, smallest numbers divisible by the numbers 1 to 8, sparsely totient number, Harshad number in base 2 through base 10

841 = 29² = 20² + 21², sum of three consecutive primes (277 + 281 + 283), sum of nine consecutive primes (73 + 79 + 83 + 89 + 97 + 101 + 103 + 107 + 109), centered square number, centered heptagonal number, centered octagonal number

842 = 2 × 421, nontotient

843 = 3 × 281

844 = 2² × 211, nontotient

845 = 5 × 13²

846 = 2 × 3² × 47, sum of eight consecutive primes (89 + 97 + 101 + 103 + 107 + 109 + 113 + 127), nontotient, Harshad number

847 = 7 × 11²

848 = 2⁴ × 53

849 = 3 × 283, Mertens function(849) returns 0

850 = 2 × 5² × 17, Mertens function(850) returns 0, nontotient, the maximum possible Fair Isaac credit score.

851 = 23 × 37

852 = 2² × 3 × 71, Smith number

853 prime number, Mertens function(853) returns 0, average of first 853 prime numbers is an integer (sequence A045345 in OEIS), strictly non-palindromic number

854 = 2 × 7 × 61, nontotient

855 = 3² × 5 × 19, decagonal number, centered cube number

856 = 2³ × 107, nonagonal number, centered pentagonal number

857 prime number, sum of three consecutive primes (281 + 283 + 293), Chen prime, Eisenstein prime with no imaginary part

858 = 2 × 3 × 11 × 13, Giuga number

859 prime number

860 = 2² × 5 × 43, sum of four consecutive primes (199 + 211 + 223 + 227)

861 = 3 × 7 × 41, sphenic number, triangular number, hexagonal number, Smith number

862 = 2 × 431

863 prime number, safe prime, sum of five consecutive primes (163 + 167 + 173 + 179 + 181), sum of seven consecutive primes (107 + 109 + 113 + 127 + 131 + 137 + 139), Chen prime, Eisenstein prime with no imaginary part

864 = 2⁵ × 3³, sum of a twin prime (431 + 433), sum of six consecutive primes (131 + 137 + 139 + 149 + 151 + 157), Harshad number

865 = 5 × 173

866 = 2 × 433, nontotient

867 = 3 × 17²

868 = 2² × 7 × 31, nontotient

869 = 11 × 79, Mertens function(869) returns 0

870 = 2 × 3 × 5 × 29, sum of ten consecutive primes (67 + 71 + 73 + 79 + 83 + 89 + 97 + 101 + 103 + 107), pronic number, nontotient, sparsely totient number, Harshad number

This number is the magic constant of n×n normal magic square and n-queens problem for n = 12.

871 = 13 × 67

872 = 2³ × 109, nontotient

873 = 3² × 97, sum of the first six factorials from 1

874 = 2 × 19 × 23, sum of the first twenty-three primes, sum of the first seven factorials from 0, nontotient, Harshad number

875 = 5³ × 7

876 = 2² × 3 × 73

877 prime number, Bell number, Chen prime, Mertens function(877) returns 0, strictly non-palindromic number.

878 = 2 × 439, nontotient

879 = 3 × 293

880 = 2⁴ × 5 × 11, Harshad number; 148-gonal number; the number of n×n magic squares for n = 4.

881 prime number, twin prime, sum of nine consecutive primes (79 + 83 + 89 + 97 + 101 + 103 + 107 + 109 + 113), Chen prime, Eisenstein prime with no imaginary part

882 = 2 × 3² × 7², Harshad number, totient sum for first 53 integers

883 prime number, twin prime, sum of three consecutive primes (283 + 293 + 307), Mertens function(883) returns 0

884 = 2² × 13 × 17, Mertens function(884) returns 0

885 = 3 × 5 × 59, sphenic number

886 = 2 × 443, Mertens function(886) returns 0

887 prime number followed by primal gap of 20, safe prime, Chen prime, Eisenstein prime with no imaginary part

888 = 2³ × 3 × 37, sum of eight consecutive primes (97 + 101 + 103 + 107 + 109 + 113 + 127 + 131), Harshad number.

889 = 7 × 127, Mertens function(889) returns 0

890 = 2 × 5 × 89, sphenic number, sum of four consecutive primes (211 + 223 + 227 + 229), nontotient

891 = 3⁴ × 11, sum of five consecutive primes (167 + 173 + 179 + 181 + 191), octahedral number

892 = 2² × 223, nontotient

893 = 19 × 47, Mertens function(893) returns 0

894 = 2 × 3 × 149, sphenic number, nontotient

895 = 5 × 179, Smith number, Woodall number, Mertens function(895) returns 0

896 = 2⁷ × 7, sum of six consecutive primes (137 + 139 + 149 + 151 + 157 + 163), Mertens function(896) returns 0

897 = 3 × 13 × 23, sphenic number

898 = 2 × 449, Mertens function(898) returns 0, nontotient

899 = 29 × 31